28.搜索加速技巧

发表于 更新于 分类于 ，

搜索加速技巧

双向搜索、A、IDA等 BFS、DFS 的改进策略。

双向BFS

回顾BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct Node {
    int x, y;
    Node() { x = y = 0; }
    Node(int x_, int y_) {
        x = x_;
        y = y_;
    }
};
int BFS(int startX, int startY) {
    std::queue<Node> q;
    q.push(Node(startX, startY));
    visited[startX][startY] = true;
    while (!q.empty()) {
        Node now = q.front();
        q.pop();
        if (now.x == endX && now.y == endY) return true;
        for (int i = 0; i < 4; i++) {
            int nextX = now.x + dx[i], nextY = now.y + dy[i];
            if (graph[nextX][nextY] && !visited[nextX][nextY]) {
                visited[nextX][nextY] = true;
                q.push(Node(nextX, nextY));
            }
        }
    }
    return false;
}

BFS利用队列实现从一点出发，一层一层外扩式搜索。

当知道起点与终点，目的是找到合法最短路时，从起点和终点同时搜索可以极大减小搜索空间。

相比单向BFS,双向BFS可以大大减少搜索空间。假设单向广搜需要搜索到第d层才能到达终点,搜索空间约为\(b^d\)(b为每个节点平均分支数)。而双向广搜只需要各自搜索到第d/2层,搜索空间约为\(2b^{d/2}\),远小于\(b^d\)。

双向DFS

思想类似，如回溯枚举子集找最优解的问题中，搜索一部分元素的所有子集，再搜索另一部分元素的所有子集，进而拼凑符合条件的方案，也能指数级降低复杂度。

例：重量背包

\(n\) 个物品，每个物品有一定重量，在不超过背包容量前提下，最多装多少重量的物品。

思路：

  • 回溯枚举前半数物品所有子集，记录能凑出的所有重量，记录并排序。
  • 回溯枚举后半数物品的所有子集，每得到一个子集，用背包容量减去这个子集的重量，剩余重量二分查找前半数物品能凑出的不超出的最大值。

A*

A*是BFS的改进算法，将BFS的队列改为优先级队列，其优先级是一个“启发式”的函数，每个节点的优先级为:

\(f(n) = g(n) + h(n)\)

其中: - \(g(n)\)是从起点到当前节点\(n\)的实际代价 - \(h(n)\)是从当前节点\(n\)到终点的估计代价(启发函数)

常见的启发函数:

  • 曼哈顿距离:适用于网格图,只能上下左右移动。两点间的曼哈顿距离为 \(|x1-x2| + |y1-y2|\)，即横向和纵向距离之和
  • 欧几里得距离:适用于八方向移动。两点间的欧几里得距离为 \(sqrt((x1-x2)^2 + (y1-y2)^2)\)，即直线距离
  • 对角线距离:适用于网格图,可以斜向移动。两点间的对角线距离为 \(max(|x1-x2|, |y1-y2|)\)，因为可以斜着走,只需要走最长的那条边的距离

A*算法相比BFS,通过启发函数引导搜索朝目标方向进行,可以大大减少搜索空间。但如果启发函数设计不当,可能会失去最优性。

例：八数码

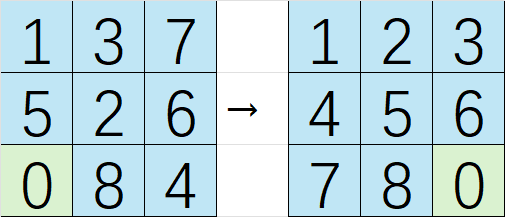
九宫格放\(1\sim 8\)八个数，一个空格可以看作\(0\)，\(0\)周围的格子可以移到\(0\)上，找一个移动方案将\(1\sim 8\)归位到从上到下、从左到右按顺序的排列。

\(h\) 函数可以定义为每个数距离目标位置的曼哈顿距离、不在应该在的位置的棋子个数等。

迭代加深（IDDFS）

“以DFS方式实现的BFS”

BFS从近到远一点点向外搜索，用队列实现。而IDDFS也是从近到远一点点扩大搜索范围，每次限制一个DFS深度，进行DFS，到达深度就返回，搜完没找到答案时，扩大深度限制，再进行一次DFS。

当BFS的搜索空间过大时，考虑用IDDFS，适合场景：

  • 解的深度未知
  • 搜索空间巨大
  • 内存受限

IDA*

IDA*是迭代加深搜索(IDDFS)和A*的结合。它使用迭代加深的框架，但每次深度限制不是搜索深度，而是启发函数值的限制。

具体来说:

  1. 设定初始的启发函数值限制
  2. 用DFS方式搜索,但当 \(f(n) = g(n) + h(n)\) 超过限制时就返回
  3. 如果没找到解，增大启发函数值限制，重新搜索
  4. 重复以上步骤直到找到解

IDA*相比A*的优点:

  • 空间复杂度低,因为用DFS实现
  • 不需要维护开放列表和关闭列表
  • 适合搜索空间巨大的问题

缺点是可能会重复搜索一些状态。